I've started playing with algorithms recently. I've felt a little bit rusty (I must admit that in my daily work I don't have to many occasions on which I would need to write some smart algorithms) so I decided to find some time in order to solve one former Codility challenge every week (you can find the solutions in my GitHub repository). Recently Codility have started publishing a programming course and some "further training" tasks. As I was looking through those one have dragged mine attention: Array Inversions Count. The task requirements are clearly screaming Mergesort, so I thought it is a great chance to see how good can I implement an old school algorithm in C#.

Codility is running its tests on Mono platform. I have done some testing which confirms the same behavior on Microsoft .Net Framework but I still feel that I should note this.

Mergesort is a classic algorithm which follows divide and conquer paradigm. It boils down to splitting and merging arrays with some reorganization along the way. I doubt I can explain it better than Wikipedia does, so I will go straight to the first implementation that came into my mind.

private int[] MergeSort(int[] A, out int inversionsCount)
{
  inversionsCount = 0;

  int[] sortedArray;
  if (A.Length == 1)
    sortedArray = A;
  //If the length of input array is greater than one
  else
  {
    int lowerArrayInversionsCount = 0, upperArrayInversionsCount = 0;
    int lowerArrayIndex = 0, upperArrayIndex = 0;

    //Split the array into lower half
    int[] lowerArray = new int[A.Length / 2];
    Array.Copy(A, lowerArray, lowerArray.Length);
    //Which will be sorted recursively
    lowerArray = MergeSort(lowerArray, out lowerArrayInversionsCount);

    //And upper half
    int[] upperArray = new int[A.Length - lowerArray.Length];
    Array.Copy(A, lowerArray.Length, upperArray, 0, upperArray.Length);
    //Which also will be sorted recursively
    upperArray = MergeSort(upperArray, out upperArrayInversionsCount);

    inversionsCount = lowerArrayInversionsCount + upperArrayInversionsCount;

    //The sorted array is a result of proper merging of the lower and upper half
    sortedArray = new int[A.Length];
    lowerArrayIndex = 0;
    upperArrayIndex = 0;
    //For all the elements
    for (int sortedArrayIndex = 0; sortedArrayIndex < sortedArray.Length; sortedArrayIndex++)
    {
      //If all the elements from lower half has been copied
      if (lowerArrayIndex == lowerArray.Length)
        //Copy the element from upper half
        sortedArray[sortedArrayIndex] = upperArray[upperArrayIndex++];
      //If all the elements from upper half has been copied
      else if (upperArrayIndex == upperArray.Length)
        //Copy the element from lower half
        sortedArray[sortedArrayIndex] = lowerArray[lowerArrayIndex++];
      //If the current element in lower half is less or equal than current element in upper half
      else if (lowerArray[lowerArrayIndex] <= upperArray[upperArrayIndex])
        //Copy the element from lower half
        sortedArray[sortedArrayIndex] = lowerArray[lowerArrayIndex++];
      //In any other case
      else
      {
        //Copy the element from upper half
        sortedArray[sortedArrayIndex] = upperArray[upperArrayIndex++];
        //And count the inversions
        inversionsCount += lowerArray.Length - lowerArrayIndex;
      }
    }
  }

  return sortedArray;
}

The above implementation gives following results on Codility:

So the implementation is correct. Now it is time for the fun part, how can I make it faster? There is one place where I'm letting framework do some work for me - calling Array.Copy while creating lower and upper arrays. The .Net Framework provides also a Buffer.BlockCopy method which is a more low-level way of copying arrays and as such might prove to give better performance. So I've changed calls to Array.Copy into proper calls to Buffer.BlockCopy.

private const int _intSize = 4;

public int[] MergeSort(int[] A, out int inversionsCount)
{
  ...

  //Array.Copy(A, lowerArray, lowerArray.Length);
  Buffer.BlockCopy(A, 0, lowerArray, 0, lowerArray.Length * _intSize);
  ...

  //Array.Copy(A, lowerArray.Length, upperArray, 0, upperArray.Length);
  Buffer.BlockCopy(A, lowerArray.Length * _intSize, upperArray, 0, upperArray.Length * _intSize);
  ...
}

The results for this implementation are exactly the same as for the Array.Copy. In other words there is no noticeable performance gain or loss. In that case I decided I would like to see what happens if I copy the arrays myself (with good old for loop). Quick change in the source code.

public int[] MergeSort(int[] A, out int inversionsCount)
{  
  ...

  //Array.Copy(A, lowerArray, lowerArray.Length);
  for (lowerArrayIndex = 0; lowerArrayIndex < lowerArray.Length; lowerArrayIndex++)
    lowerArray[lowerArrayIndex] = A[lowerArrayIndex];
  ...

  //Array.Copy(A, lowerArray.Length, upperArray, 0, upperArray.Length);
  for (upperArrayIndex = 0; upperArrayIndex < upperArray.Length; upperArrayIndex++)
    upperArray[upperArrayIndex] = A[lowerArrayIndex + upperArrayIndex];
  ...
}

And voila.

Honestly I wasn't expecting this. The implementation shows a little bit better performance with big sets of data. So the for loop seems to be copying arrays faster than framework functions in this case.

All this focus on copying arrays made me wonder; Do I even need to copy those arrays in the first place? It is probably enough to keep track of witch part of the original array I need to work on. This thought brought me to the following solution.

private int[] MergeSort(int[] A, int startIndex, int endIndex, out int inversionsCount)
{  
  inversionsCount = 0;

  int[] sortedArray;
  //If the part of the array that needs sorting is just one element
  if (startIndex >= endIndex)
    //Return new array
    sortedArray = new int[] { A[endIndex] };
  //Otherwise
  else
  {  
    //Calculate the index of the last element in the lower subpart of the array
    int lowerArrayEndIndex = (startIndex + endIndex) / 2;
    int lowerArrayInversionsCount = 0, upperArrayInversionsCount = 0;

    //Recursively sort the lower and upper subparts of the array
    int[] lowerArray = MergeSort(A, startIndex, lowerArrayEndIndex, out lowerArrayInversionsCount);
    int[] upperArray = MergeSort(A, lowerArrayEndIndex + 1, endIndex, out upperArrayInversionsCount);

    inversionsCount = lowerArrayInversionsCount + upperArrayInversionsCount;

    //The result will be new array, which will be creating by merging lower and upper subpart
    sortedArray = new int[endIndex - startIndex + 1];
    int lowerArrayIndex = 0, upperArrayIndex = 0;
    //For every index in the original array
    for (int sortedArrayIndex = 0; sortedArrayIndex < sortedArray.Length; sortedArrayIndex++)
    {
      //If all the elements from lower subpart has been merged
      if (lowerArrayIndex == lowerArray.Length)
        //Add the element from upper subpart to the sorted array
        sortedArray[sortedArrayIndex] = upperArray[upperArrayIndex++];
      //If all the elements from upper subpart has been merged
      else if (upperArrayIndex == upperArray.Length)
        //Add the element from lower subpart to the sorted array
        sortedArray[sortedArrayIndex] = lowerArray[lowerArrayIndex++];
      //If first not merged element in lower subpart is smaller than first not merged element in upper subpart
      else if (lowerArray[lowerArrayIndex] <= upperArray[upperArrayIndex])
        //Add the element from lower subpart to the sorted array
        sortedArray[sortedArrayIndex] = lowerArray[lowerArrayIndex++];
      //If first not merged element in upper subpart is smaller than first not merged element in lower subpart
      else
      {
        //Add the element from upper subpart to the sorted array
        sortedArray[sortedArrayIndex] = upperArray[upperArrayIndex++];
        //And count the inversions
        inversionsCount += lowerArray.Length - lowerArrayIndex;
      }
    }
  }

  //Return sorted array (part)
  return sortedArray;
}

This should improve the performance, so let's see the results.

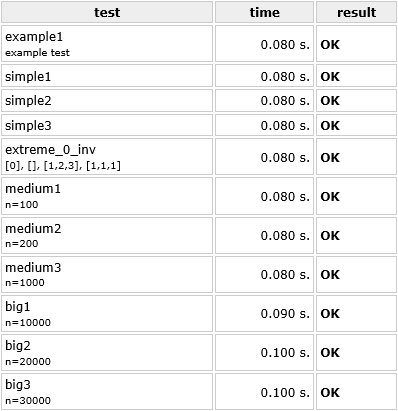
The improvement for big data sets is there. If it comes to smaller input arrays, there is no change. This can lead to the conclusion that in cases of smaller data sets the operation of copying arrays doesn't have much influence on overall execution time (but the space complexity is better with this implementation so it is worth the effort).

Probably for most of you what I have described above is nothing new. For a person like me (who doesn't have many chances to play with algorithms like this) it was fun and educating experience. This is why I decided to write it down - maybe (just maybe) somebody else will find it useful or interesting.